堆排序

数组、链表都是一维的数据结构，相对来说比较容易理解，而堆是二维的数据结构，对抽象思维的要求更高，所以许多程序员「谈堆色变」。但堆又是数据结构进阶必经的一步，我们不妨静下心来，将其梳理清楚。

堆：符合以下两个条件之一的完全二叉树：

  • 根节点的值 ≥ 子节点的值，这样的堆被称之为最大堆，或大顶堆；
  • 根节点的值 ≤ 子节点的值，这样的堆被称之为最小堆，或小顶堆。

堆排序过程如下：

  • 用数列构建出一个大顶堆，取出堆顶的数字；
  • 调整剩余的数字，构建出新的大顶堆，再次取出堆顶的数字；
  • 循环往复，完成整个排序。

整体的思路就是这么简单，我们需要解决的问题有两个：

  • 如何用数列构建出一个大顶堆；
  • 取出堆顶的数字后，如何将剩余的数字调整成新的大顶堆。

构建大顶堆 & 调整堆

构建大顶堆有两种方式：

  1. 方案一：从 0 开始，将每个数字依次插入堆中，一边插入，一边调整堆的结构，使其满足大顶堆的要求；
  2. 方案二：将整个数列的初始状态视作一棵完全二叉树，自底向上调整树的结构，使其满足大顶堆的要求。

方案二更为常用，动图演示如下：

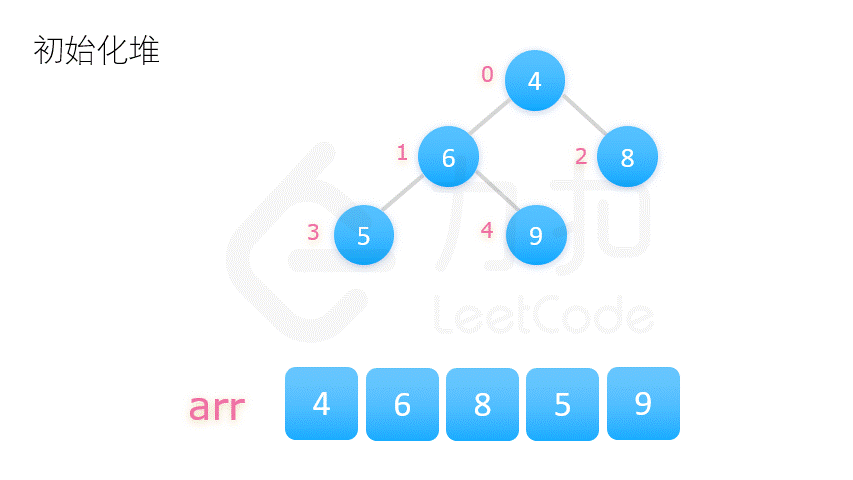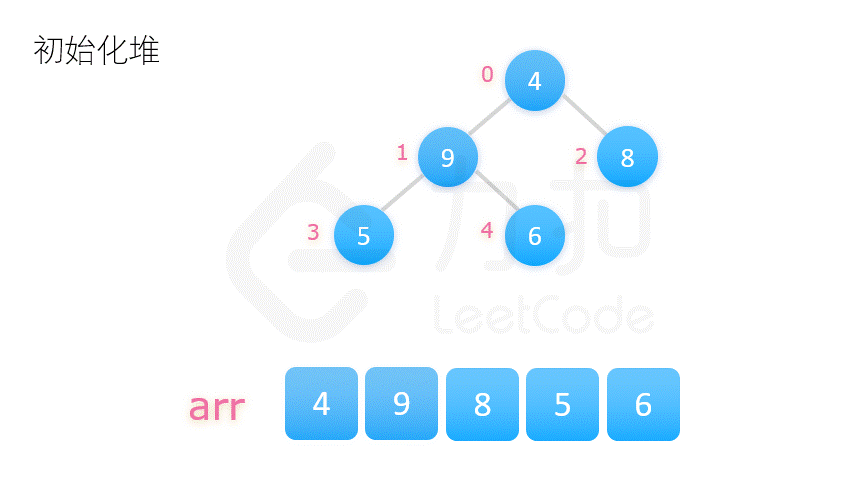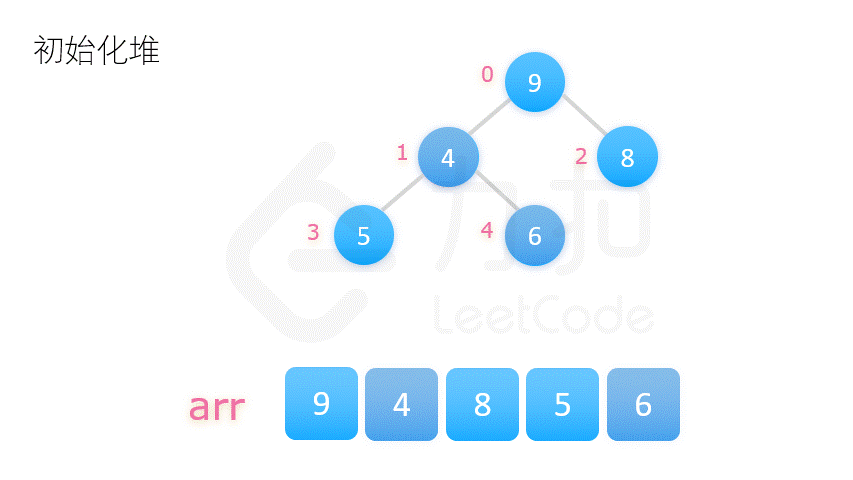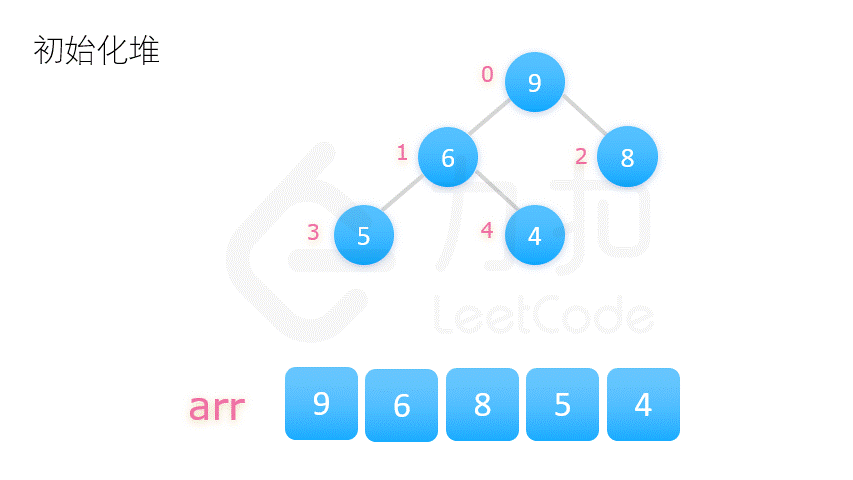
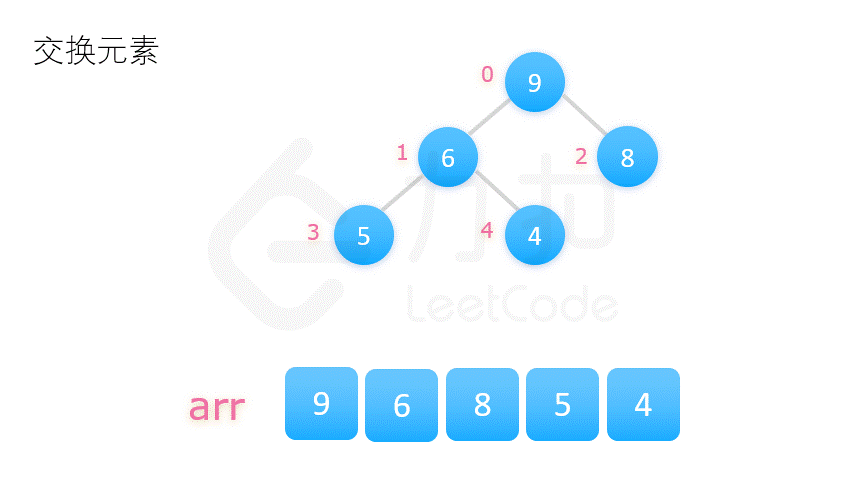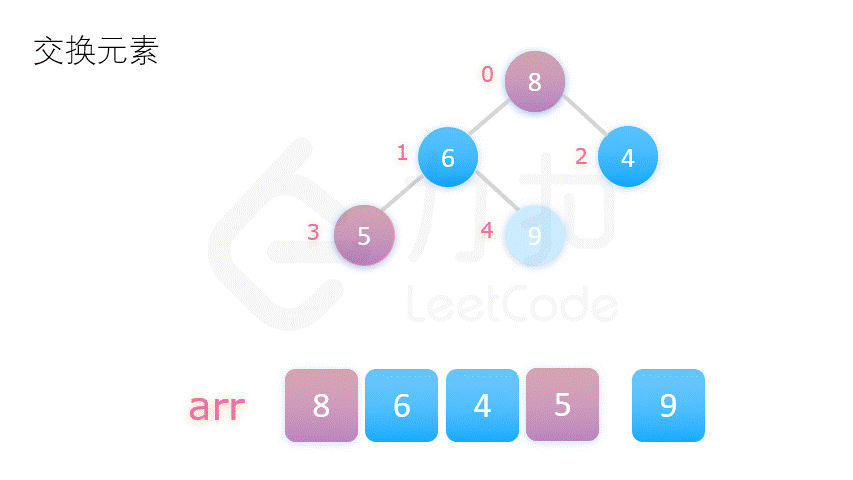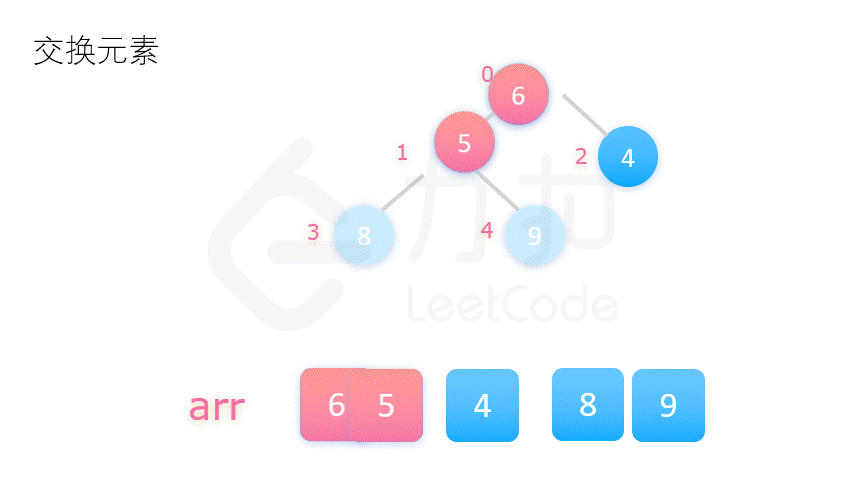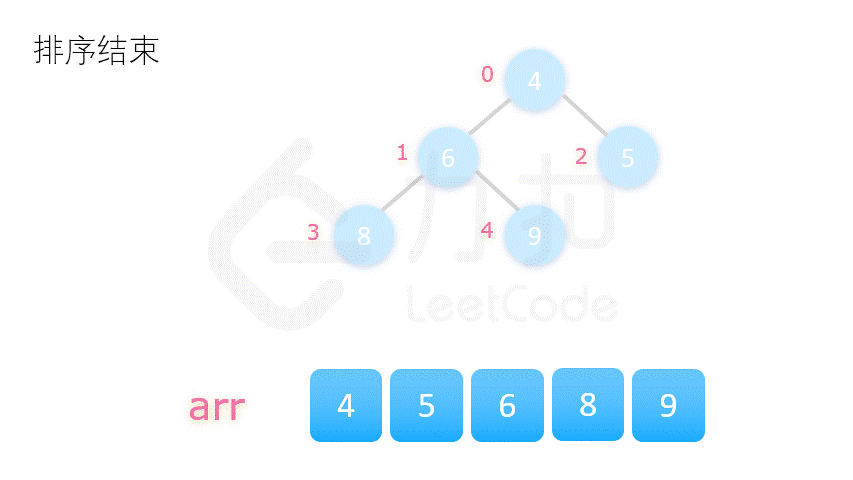
Alt text

Alt text

在介绍堆排序具体实现之前，我们先要了解完全二叉树的几个性质。将根节点的下标视为 0，则完全二叉树有如下性质：

  • 对于完全二叉树中的第 i 个数，它的左子节点下标：left = 2i + 1
  • 对于完全二叉树中的第 i 个数，它的右子节点下标：right = left + 1
  • 对于有 n 个元素的完全二叉树 (n≥2)，它的最后一个非叶子结点的下标：n/2 - 1

堆排序代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public static void heapSort(int[] arr) {
    // 构建初始大顶堆
    buildMaxHeap(arr);
    for (int i = arr.length - 1; i > 0; i--) {
        // 将最大值交换到数组最后
        swap(arr, 0, i);
        // 调整剩余数组，使其满足大顶堆
        maxHeapify(arr, 0, i);
    }
}
// 构建初始大顶堆
private static void buildMaxHeap(int[] arr) {
    // 从最后一个非叶子结点开始调整大顶堆，最后一个非叶子结点的下标就是 arr.length / 2-1
    for (int i = arr.length / 2 - 1; i >= 0; i--) {
        maxHeapify(arr, i, arr.length);
    }
}
// 调整大顶堆，第三个参数表示剩余未排序的数字的数量，也就是剩余堆的大小
private static void maxHeapify(int[] arr, int i, int heapSize) {
    // 左子结点下标
    int l = 2 * i + 1;
    // 右子结点下标
    int r = l + 1;
    // 记录根结点、左子树结点、右子树结点三者中的最大值下标
    int largest = i;
    // 与左子树结点比较
    if (l < heapSize && arr[l] > arr[largest]) {
        largest = l;
    }
    // 与右子树结点比较
    if (r < heapSize && arr[r] > arr[largest]) {
        largest = r;
    }
    if (largest != i) {
        // 将最大值交换为根结点
        swap(arr, i, largest);
        // 再次调整交换数字后的大顶堆
        maxHeapify(arr, largest, heapSize);
    }
}
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

堆排序的第一步就是构建大顶堆，对应代码中的 buildMaxHeap 函数。我们将数组视作一颗完全二叉树，从它的最后一个非叶子结点开始，调整此结点和其左右子树，使这三个数字构成一个大顶堆。

调整过程由 maxHeapify 函数处理， maxHeapify 函数记录了最大值的下标，根结点和其左右子树结点在经过比较之后，将最大值交换到根结点位置。这样，这三个数字就构成了一个大顶堆。

需要注意的是，如果根结点和左右子树结点任何一个数字发生了交换，则还需要保证调整后的子树仍然是大顶堆，所以子树会执行一个递归的调整过程。

当构建出大顶堆之后，就要把冠军交换到数列最后，深藏功与名。来到冠军宝座的新人又要开始向下比较，找到自己的真实位置，使得剩下的 n−1 个数字构建成新的大顶堆。这就是 heapSort 方法的 for 循环中，调用 maxHeapify 的原因。

变量 heapSize 用来记录还剩下多少个数字没有排序完成，每当交换了一个堆顶的数字，heapSize 就会减 1。在 maxHeapify 方法中，使用 heapSize 来限制剩下的选手，不要和已经躺在数组最后最大的值比较。

这就是堆排序的思想。学习时我们采用的是最简单的代码实现，在熟练掌握了之后我们就可以加一些小技巧以获得更高的效率。比如我们知道计算机采用二进制来存储数据，数字左移一位表示乘以 2
2，右移一位表示除以 2。所以堆排序代码中的arr.length / 2 - 1 可以修改为 (arr.length >> 1) - 1，左子结点下标2 * i + 1可以修改为(i << 1) + 1。需要注意的是，位运算符的优先级比加减运算的优先级低，所以必须给位运算过程加上括号。

注：在有的文章中，作者将堆的根节点下标视为 1，这样做的好处是使得第 i 个结点的左子结点下标为 2i，右子结点下标为 2i + 1，与 2i + 1 和 2i + 2 相比，计算量会少一点，本文未采取这种实现，但两种实现思路的核心思想都是一致的。

分析可知，堆排序是不稳定的排序算法。

时间复杂度 & 空间复杂度

堆排序分为两个阶段：初始化建堆（buildMaxHeap）和重建堆（maxHeapify，直译为大顶堆化）。所以时间复杂度要从这两个方面分析。

根据数学运算可以推导出初始化建堆的时间复杂度为 O(n)，重建堆的时间复杂度为 O(nlogn) ，所以堆排序总的时间复杂度为 O(nlogn) 。推导过程较为复杂，故不再给出证明过程。

堆排序的空间复杂度为 O(1)，只需要常数级的临时变量。

堆排序是一个优秀的排序算法，但是在实际应用中，快速排序的性能一般会优于堆排序。