背包动态规划

背包问题（Knapsack problem）是一种组合优化的 NP 完全问题。

背包问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

这是背包问题最基础的描述，再往下细分还可以把背包问题分成几大类，其中比较基础的是 3 种：01 背包，完全背包，多重背包。

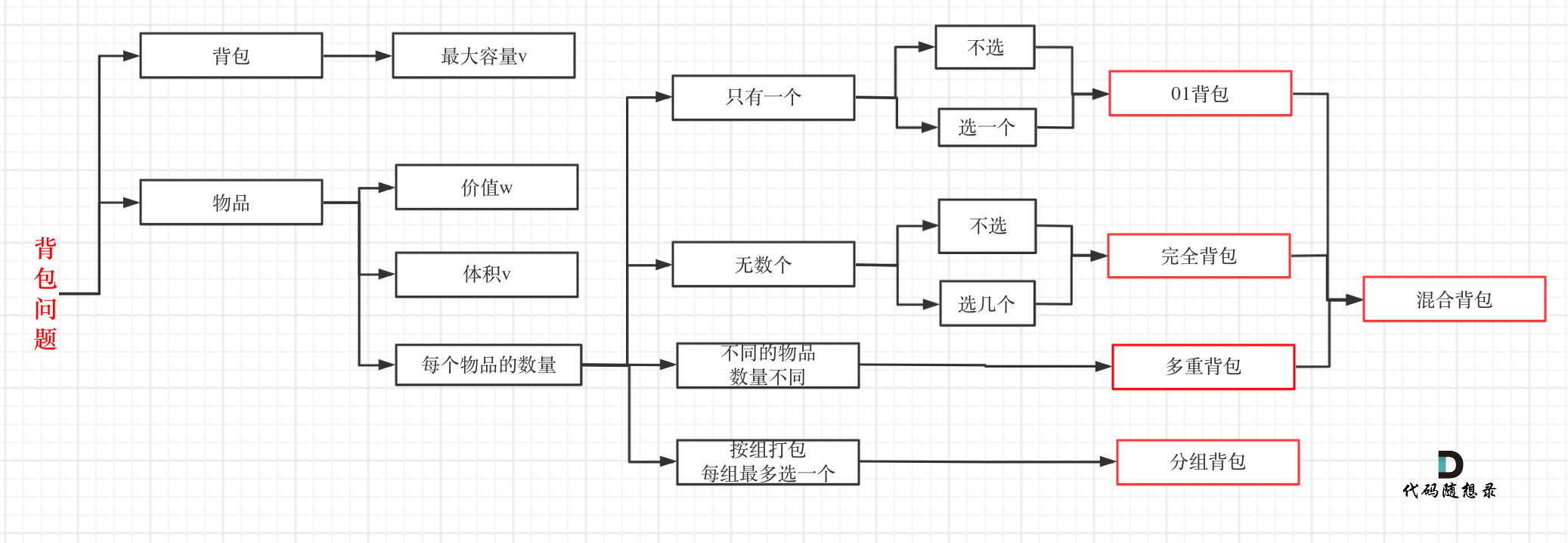
01 背包问题

有 n 种物品，物品 j 的体积为 vj，价值为 wi，有一个体积限制 V。每种物品只有 1 个，只有选或者不选，而没有选几个的问题，此问题称为 01 背包问题。

dp[i][j] := 考虑了 [0..i]  里的物品，占用了 j 空间，所能取得的最大价值。
dp[i][j] = dp[i - 1][j] 当前物品不选
           dp[i - 1][j - v[i]] + w[i] 当前物品选，j - v[i] 要大于等于 0
初始化时将所有状态置为 0 即可。           

题解，技巧在于讲 dp 初始化成 int[][] dp = new int[N + 1][V + 1];。

例题见 2. 01背包问题

// https://www.acwing.com/problem/content/submission/code_detail/21428160/
Scanner in = new Scanner(System.in);
int N = in.nextInt();  // 物品数目
int V = in.nextInt();  // 背包容积
// 状态：dp[i][j] 表示 [0...i] 的物品达到 j 体积的最高价值
// 转移：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - volume] + value)
// 初始：dp[0][j] = 0 /* 背包不要求装满 */
// 返回：dp[N][V]

// 全部状态初始化为 0
int[][] dp = new int[N + 1][V + 1];
int[] volumes = new int[N];
int[] values = new int[N];

for (int i = 0; i < N; ++i) {
    // 体积和价值
    volumes[i] = in.nextInt();
    values[i] = in.nextInt();
}
// 初始化 0
for (int i = 1; i <= N; ++i) {
    int value = values[i - 1];
    int volume = volumes[i - 1];
    for (int j = 1; j <= V; ++j)
        dp[i][j] = Math.max(dp[i - 1][j] /* 不拿 */, 
                            (j - volume < 0) ? 0 : dp[i - 1][j - volume] + value /* 拿 */);
}
System.out.print(dp[N][V]);

01 背包的终极形态

dp[j] = max(dp[j], dp[j - v[i]] + w[i]) // j 从大往小推

一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

for (int i = 0; i < nums.size(); ++i)
    for (int j = 背包容量; j >= w ; --j)    // 防止越界j >= w
        dp[j] = max(dp[j], dp[j - w] + v);

01 背包 —— 要求背包必须放满

这个问题可以在 01 背包的基础上改两个地方。

1. dp 初始化是要初始化为 -1,-1 表示方案不可取。同时 dp[0][0] = 0
2. 状态转移时，dp[i - 1][j - v[i]] + w[i] 要更新进 dp[i][j] 前，先要判断 dp[i - 1][j - v[i]] 是否为 -1，不为 -1，则 dp[i - 1][j - v[i]] 代表的物品组才能放出来

如果是第一种问法，要求恰好装满背包，那么在初始化时除了F[0]为0，其它F[1..V ]均设为−∞，这样就可以保证最终得到的F[V ]是一种恰好装满背包的最优解。

如果并没有要求必须把背包装满，而是只希望价格尽量大，初始化时应该将F[0..V ]全部设为0。

这是为什么呢？可以这样理解：初始化的F数组事实上就是在没有任何物品可以放入背包时的合法状态。如果要求背包恰好装满，那么此时只有容量为0的背包可以在什么也不装且价值为0的情况下被“恰好装满”，其它容量的背包均没有合法的解，属于未定义的状态，应该被赋值为-∞了。如果背包并非必须被装满，那么任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。

这个小技巧完全可以推广到其它类型的背包问题，后面也就不再对进行状态转移之前的初始化进行讲解。

完全背包问题

有 n 种物品，物品 j 的体积为 vj，价值为 wi，有一个体积限制 V。每种物品有无限个，此问题称为 完全背包问题。

一个朴素的思路是将完全背包强行变成 01 背包：对每个物品 i，都可以求出一个 V/v[i] ，然后就 将物品展开 ，即视为有 V/v[i] 个同样的物品，每个物品有选和不选两种选择。

但是这种办法复杂度太高了，需要优化。

1) 一个简单有效的优化

若两件物品i、j满足Ci ≤ Cj且Wi ≥ Wj，则将可以将物品j直接去掉，不用考虑。

首先将费用大于V 的物品去掉，然后使用类似计数排序的做法，计算出费用相同的物品中价值最高的是哪个，可以O(V + N)地完成这个优化。

2) 利用二进制的思想，转化为 01 背包问题求解

略。

在完全背包中，不论空间是二维，还是优化为一维，两个for循环嵌套顺序同样无所谓！因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的（左上）。只要保证下标j之前的dp[j]都是经过计算的就可以了。

完全背包的终极形态

dp[j] = max(dp[j], dp[j - v[i]] + w[i]) // j 从小往大推

背包组合、排列问题

组合数：顺序不重要

for (int i = 0; i < nums.size(); i++) { // 遍历物品
    for (int j = nums[i]; j <= amount; j++) { // 遍历背包容量
        dp[j] += dp[j - nums[i]];
    }
}

假设：nums[0] = 1，nums[1] = 5。

那么就是先把1加入计算，然后再把5加入计算，得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。

所以这种遍历顺序中dp[j]里计算的是组合数！

排列数：顺序重要

for (int j = 0; j <= amount; j++) { // 遍历背包容量
    for (int i = 0; i < nums.size(); i++) { // 遍历物品
        if (j - nums[i] >= 0) dp[j] += dp[j - nums[i]];
    }
}

背包容量的每一个值，都是经过 1 和 5 的计算，包含了{1, 5} 和 {5, 1}两种情况。

此时dp[j]里算出来的就是排列数！

组合问题举一反三

• 组合总和 Ⅳ（本题）
• 目标和
• 零钱兑换 II

多重背包问题

多重背包问题是这样描述的：

有 n 种物品，物品 j 的体积为 vj，价值为 wi，有一个体积限制 V 。每种物品还有一个 ci，表示每种物品的个数，此问题称为多重背包问题。

思路 1：将物品展开，全拆成 01

这与完全背包的朴素思路一致。与完全背包的情况一样，这种方法是正确的，但是时间复杂度较高。

多重背包的朴素算法与完全背包的朴素算法没有区别，而多重背包的优化相对较难，并且力扣上面没有多重背包的题目。下面仅对多重背包的优化做简单的介绍。

思路 2：2 进制分解

这是对思路 1 的优化。

有这样一个事实：任意一个数 n，它一定可以用 1,2,4,8,… 之间的某个数表示。例如 13 以内的所有数都可以用 1,2,4,8 表示。

所以对于物品 i, 数量限制是 ci, 可以将其分成若干物品，它们的价值和体积为：(wi, vi), (2 wi, 2 vi), ···

然后对这些物品做 01 背包。这样 01 背包的物品数就比思路 1 少很多了。这可以理解为类似于倍增法的思想。倍增法超出了力扣的范围，感兴趣的话可以找相关的资料学习。

以上就是背包动态规划的基本内容。背包动态规划在力扣上题目不多，下一节整理了 8 道背包动态规划的练习题，通过这些题可以大致了解背包问题的一些经典问题和常见的问法。

背包动态规划问题分析步骤

背包的问题常见的有三种：

1. 第一个是求最值，这是背包的原始问题，
2. 第二个是体积要取到背包容量的最值，
3. 第三个是求方案数，即组合问题。

背包问题的分析步骤：

1. 分析是否为背包问题。
2. 是背包问题三种问法中的哪一种。
3. 是 0-1 背包问题还是完全背包问题。也就是题目给的 nums 数组中的元素是否可以重复使用。
4. 如果是组合问题，即求方案数，是否需要考虑元素之间的顺序。需要考虑顺序有顺序的解法，不需要考虑顺序又有对应的解法，需要注意。

习题列表

• 零钱兑换
• 一和零
• 最后一块石头的重量 II
• 2. 01背包问题
• 3. 完全背包问题
• 4. 多重背包问题 I

总结

本文介绍了三种最基本的背包问题：01 背包，完全背包，多重背包。包括问题描述，状态设计以及状态转移方程。

实际问题会把背包问题做各种包装，而不会把问题描述的这么直白，背包的问题常见的有三种：

• 第一个是求最值，这是背包的原始问题，
• 第二个是体积要取到背包容量的最值，
• 第三个是求方案数，即组合问题。

背包问题的分析步骤：

1. 分析是否为背包问题。
2. 是背包问题三种问法中的哪一种。
3. 是 0-1 背包问题还是完全背包问题。也就是题目给的 nums 数组中的元素是否可以重复使用。
4. 如果是组合问题，即求方案数，是否需要考虑元素之间的顺序。需要考虑顺序有顺序的解法，不需要考虑顺序又有对应的解法，需要注意。

01 背包

01 背包的递推公式

dp[j] = max(dp[j], dp[j - v[i]] + w[i]) // j 从大往小推

一维dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。

for (int i = 0; i < nums.size(); ++i)
    for (int j = 背包容量; j >= w ; --j)    // 防止越界j >= w
        dp[j] = max(dp[j], dp[j - w] + v);

01 背包：要求背包必须放满

1. dp 初始化是要初始化为 -1,-1 表示方案不可取。同时 dp[0][0] = 0
2. 状态转移时，dp[i - 1][j - v[i]] + w[i] 要更新进 dp[i][j] 前，先要判断 dp[i - 1][j - v[i]] 是否为 -1，不为 -1，则 dp[i - 1][j - v[i]] 代表的物品组才能放出来

完全背包

01 背包的递推公式

dp[j] = max(dp[j], dp[j - v[i]] + w[i]) // j 从小往大推

多重背包

2 进制分解后对物品做 01 背包即可。

参考

• 『 一文搞懂完全背包问题 』从0-1背包到完全背包，逐层深入+数学推导
• 动态规划图文学