动态规划总结及练习巩固
dp 精要
在前两期中,我们介绍了动态规划的基本概念,线性动态规划,前缀和,区间动态规划,背包动态规划,状态压缩动态规划,计数动态规划,矩阵快速幂,数位动态规划。
本章我们简要回顾一下前两期的内容,首先总结一下基本概念,然后把各个题型下的题目列表整理成了思维导图方便大家回忆。如果要看详细内容或者刷题,可以翻阅动态规划精讲前两期的内容。
本期我们主要回顾线性动态规划,前缀和,区间动态规划,背包动态规划并给大家聚合题目列表。
状态压缩动态规划,计数动态规划,矩阵快速幂,数位动态规划的题目聚合列表在动态规划精讲第四期给到大家。
dp 基本概念
在动态规划精讲第一期中,我们有介绍一些基本概念,但是欠缺一点系统性。这里我们参考《算法竞赛进阶指南》中关于动态规划的讲解,把动态规划的几个核心概念梳理一下,并做一个总结。
首先我们给出思维导图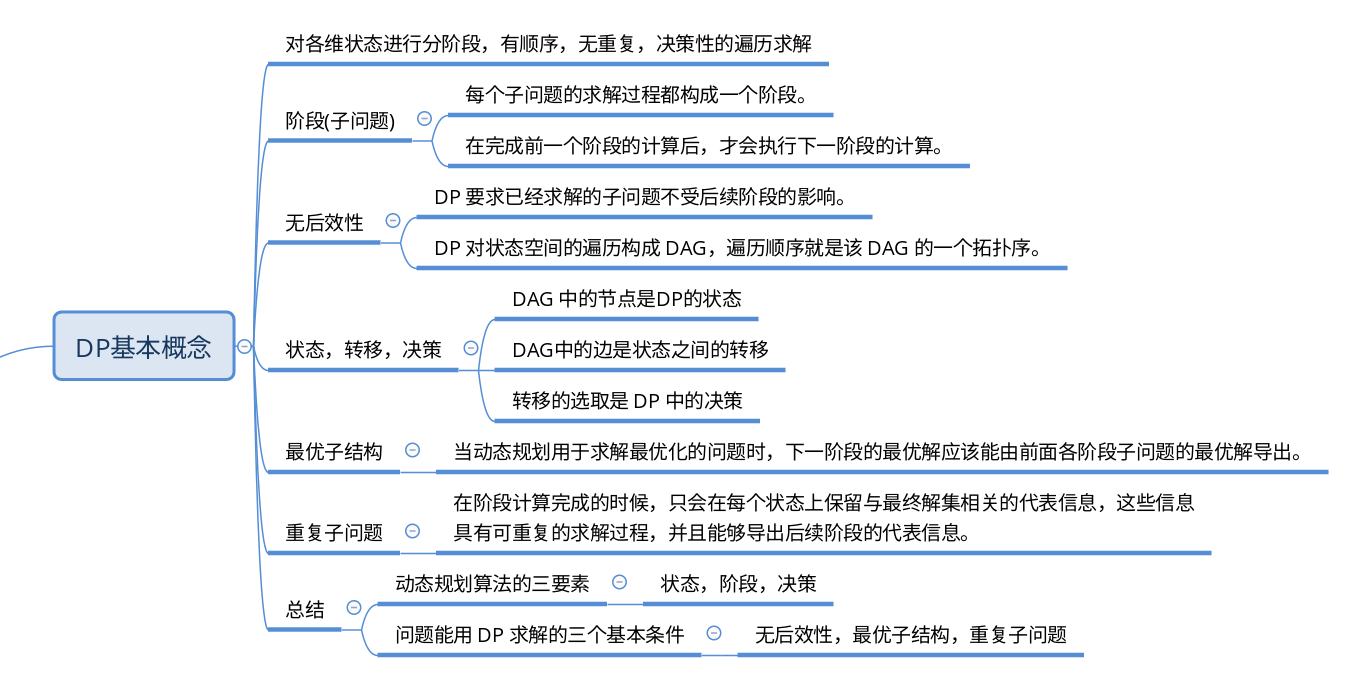
动态规划用一句话概括就是对各个状态维度进行分阶段、有顺序、无重复、决策性的遍历求解。
阶段(子问题)
动态规划把原问题视为若干个重叠子问题的逐层递进,每个子问题的求解过程都构成一个阶段。在完成前一个阶段的计算后,才会执行下一阶段的计算。
无后效性
【在完成前一个阶段的计算后,才会执行下一阶段的计算】
无后效性: 为了保证这些计算能够按顺序,不重复地进行,DP 要求已经求解的子问题不受后续阶段的影响。(后面的阶段对前面的阶段没有影响)
状态,转移,决策
由无后效性。DP 对状态空间的遍历构成 DAG,遍历顺序就是该 DAG 的一个拓扑序。DAG 中的节点对应问题的状态,边对应状态之间的转移,转移的选取是 DP 中的决策。
最优子结构
当动态规划用于求解最优化的问题时,下一阶段的最优解应该能由前面各阶段子问题的最优解导出。
重复子问题
在阶段计算完成的时候,只会在每个状态上保留与最终解集相关的代表信息,这些信息具有可重复的求解过程,并且能够导出后续阶段的代表信息。
总结
状态,阶段,决策是动态规划算法的三要素。
无后效性,最优子结构,重复子问题是问题能用 DP 求解的三个基本条件。
分阶段
动态规划是对各维状态进行分阶段,有顺序,无重复,决策性的遍历求解,其中对阶段进行划分后,每个阶段就是一个子问题。
动态规划算法有不同的阶段划分和推导的方式,常见的阶段划分方式如下:
「线性 DP」: 具有线性阶段划分的 DP 问题
「树形 DP」: 以节点的深度作为阶段的 DP 问题
「图上 DP」: 以节点在图上的拓扑序作为阶段的 DP 问题
这是一个广义的概念,与线性空间类似,如果一个 DP 算法的状态包含多个维度,但是各个维度上具有线性变化的阶段,也是「线性 DP」,例如背包问题,「区间 DP」均属于这种情况。
下面我们看一下「线性 DP」中常见的阶段划分方式,以此作为对前两期内容的复习。
(1)单串阶段划分
代表问题:最长上升子序列;
状态表示:dp[i] := 以 s[i] 结尾的最长上升子序列长度;
阶段划分:子序列的结尾位置,从前到后。
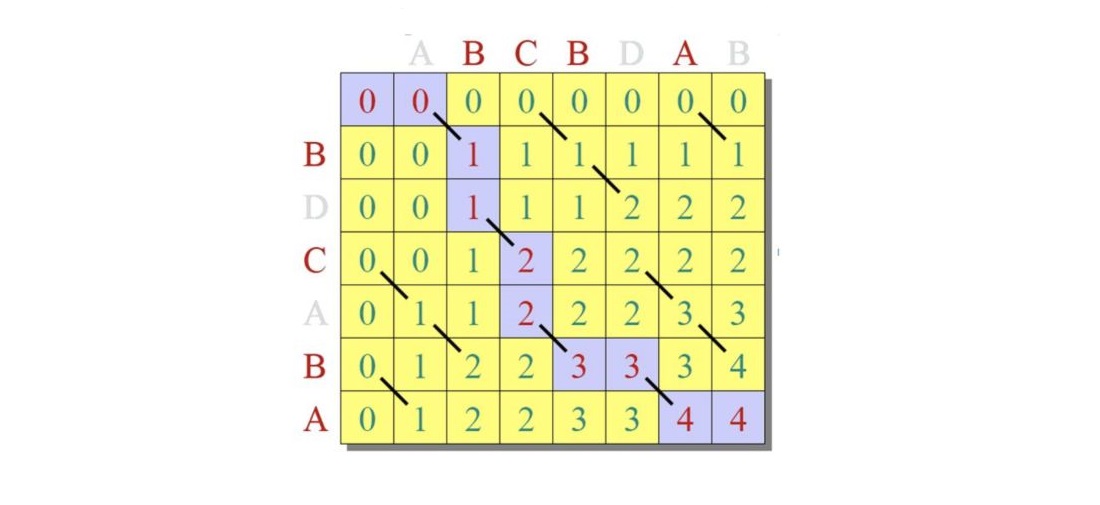
(2)双串阶段划分
代表问题:最长公共子序列;
状态表示:dp[i][j] := s[0..i], t[0..j]的最长公共子序列长度;
阶段划分:s 和 t 分别已经处理的长度,二维。
(3)棋盘阶段划分
代表问题:数字三角形;
状态表示:dp[i][j] := 从 (0, 0) 走到 (i, j) 的最大的和;
阶段划分:路径的结尾位置(矩阵中的行列位置),二维。
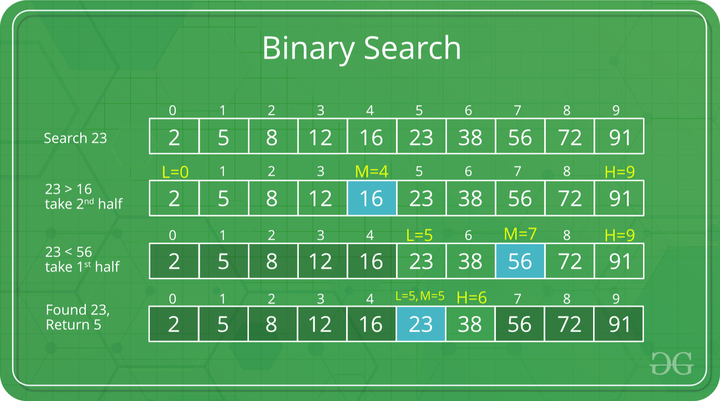
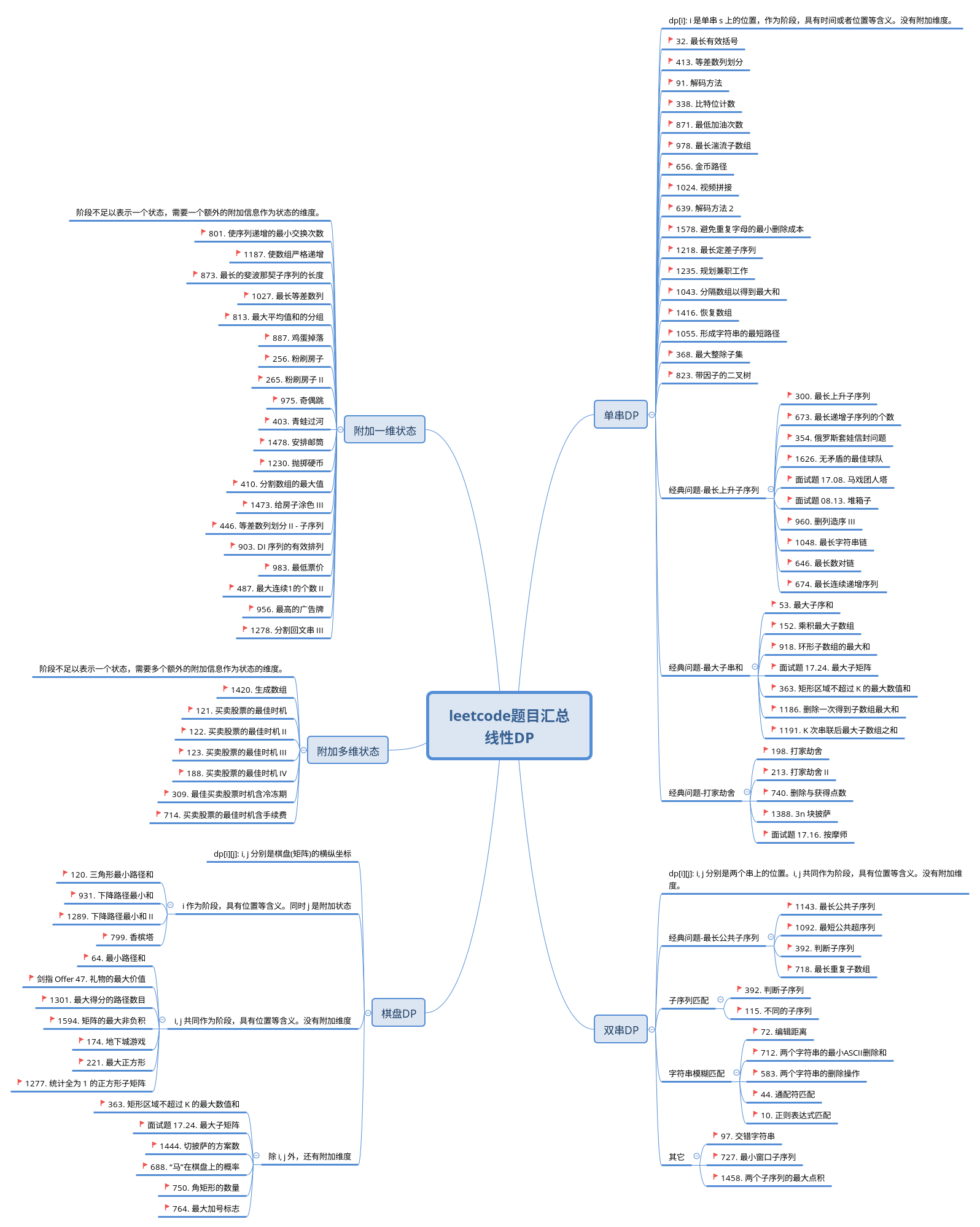
线性动态规划
「单串 DP」
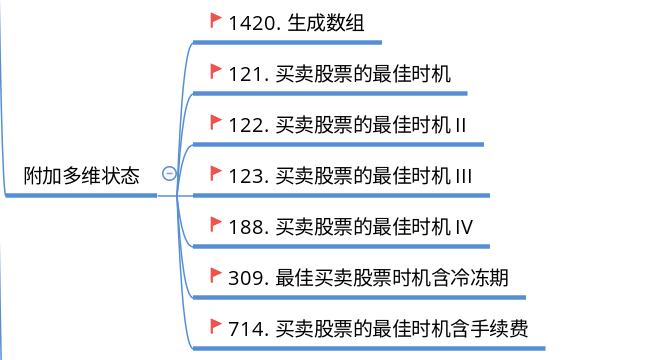
对于「单串线性 DP」问题,i 是单串 s 上的位置。作为阶段具有时间或者位置等含义。有时只有单串上的位置不足以表示状态,需要同时附加一个维度 k,一般 k 有长度、个数、次数、颜色等含义。另,所附加的维度有时候可以是多个,如 k1, k2, …
没有附加状态维度
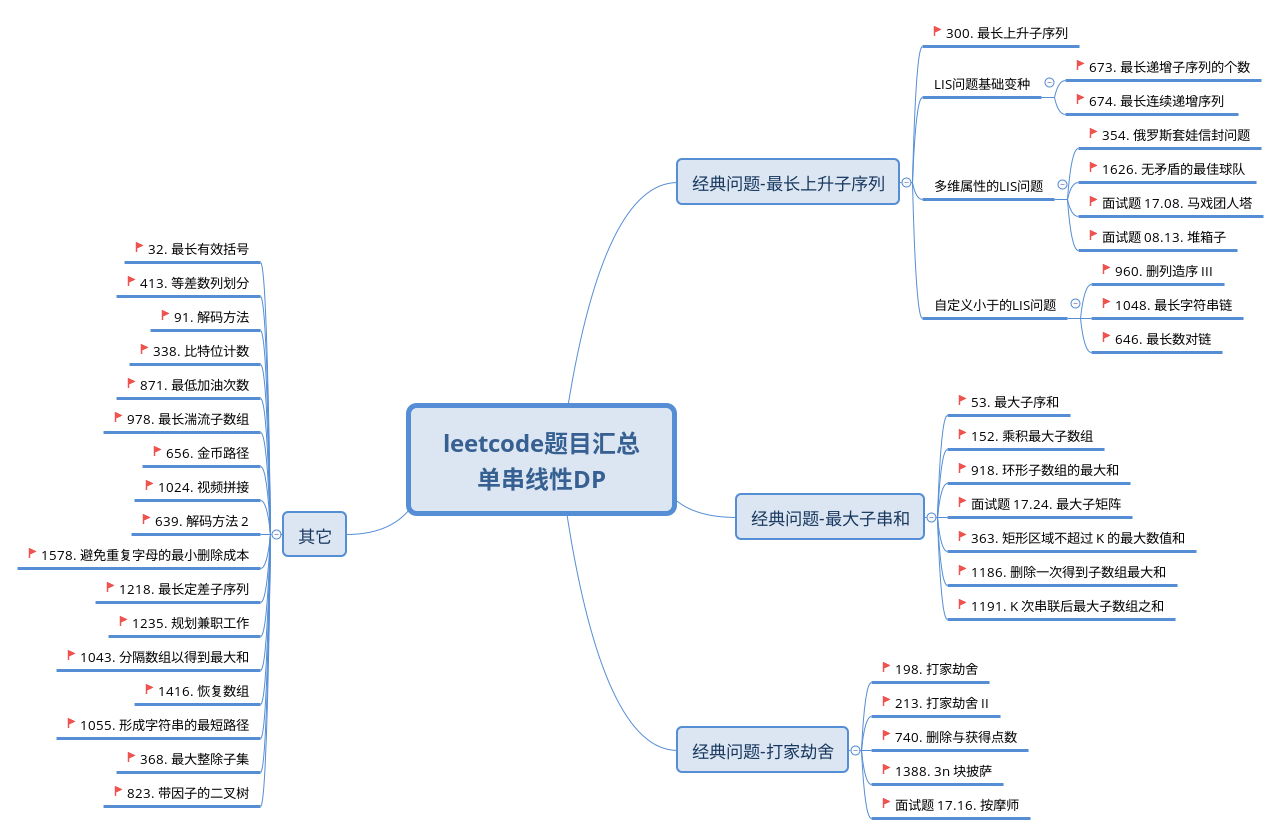
附加一维状态

附加多维状态
「双串 DP」
dp[i][j]: i, j 分别是两个串上的位置。i, j 共同作为阶段,具有位置等含义。没有附加维度。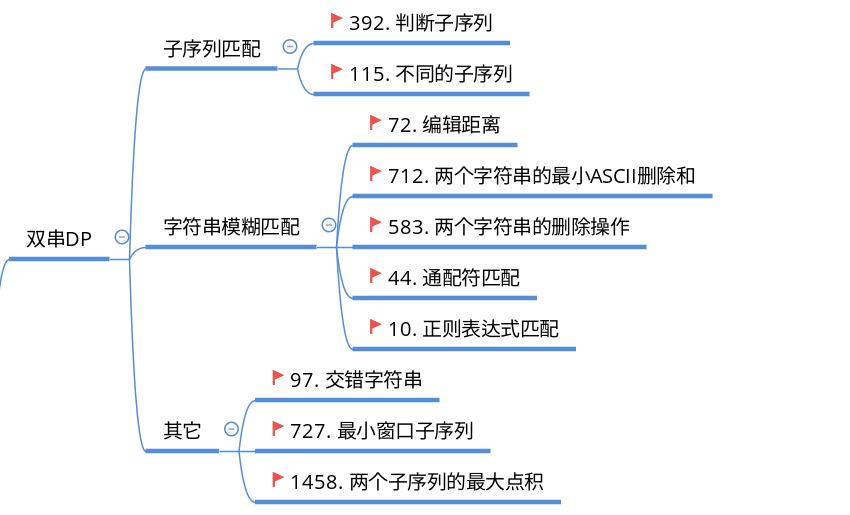
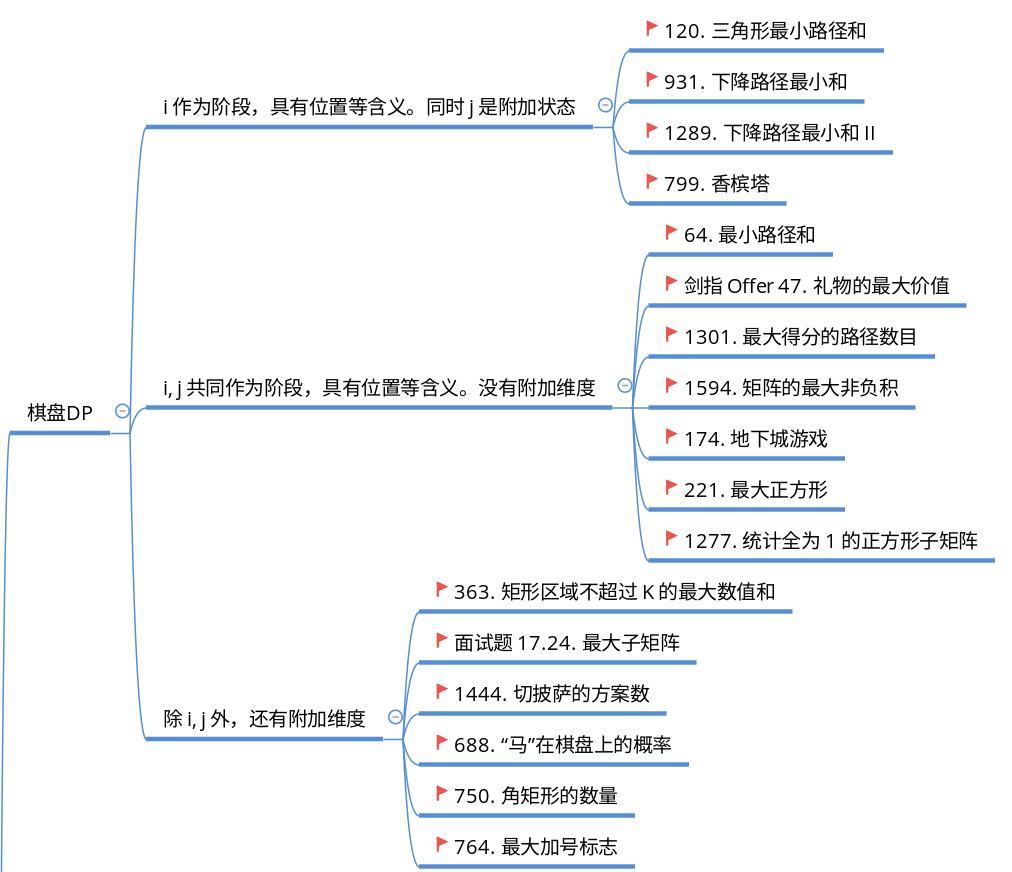
「棋盘 DP」
dp[i][j]: i, j 分别是棋盘(矩阵)的横纵坐标。阶段划分常见的两种情况分别为:
(1)i 作为阶段,具有位置等含义。j 是附加状态。
(2)i, j 共同作为阶段,具有位置等含义。没有附加维度。
「线性 DP」总结
下图是 Leetcode 上「线性 DP」的题目分类汇总,方便大家从整体上把握题目。其中不含「区间 DP」,「背包 DP」和前缀和。这三块将分别有专题汇总。
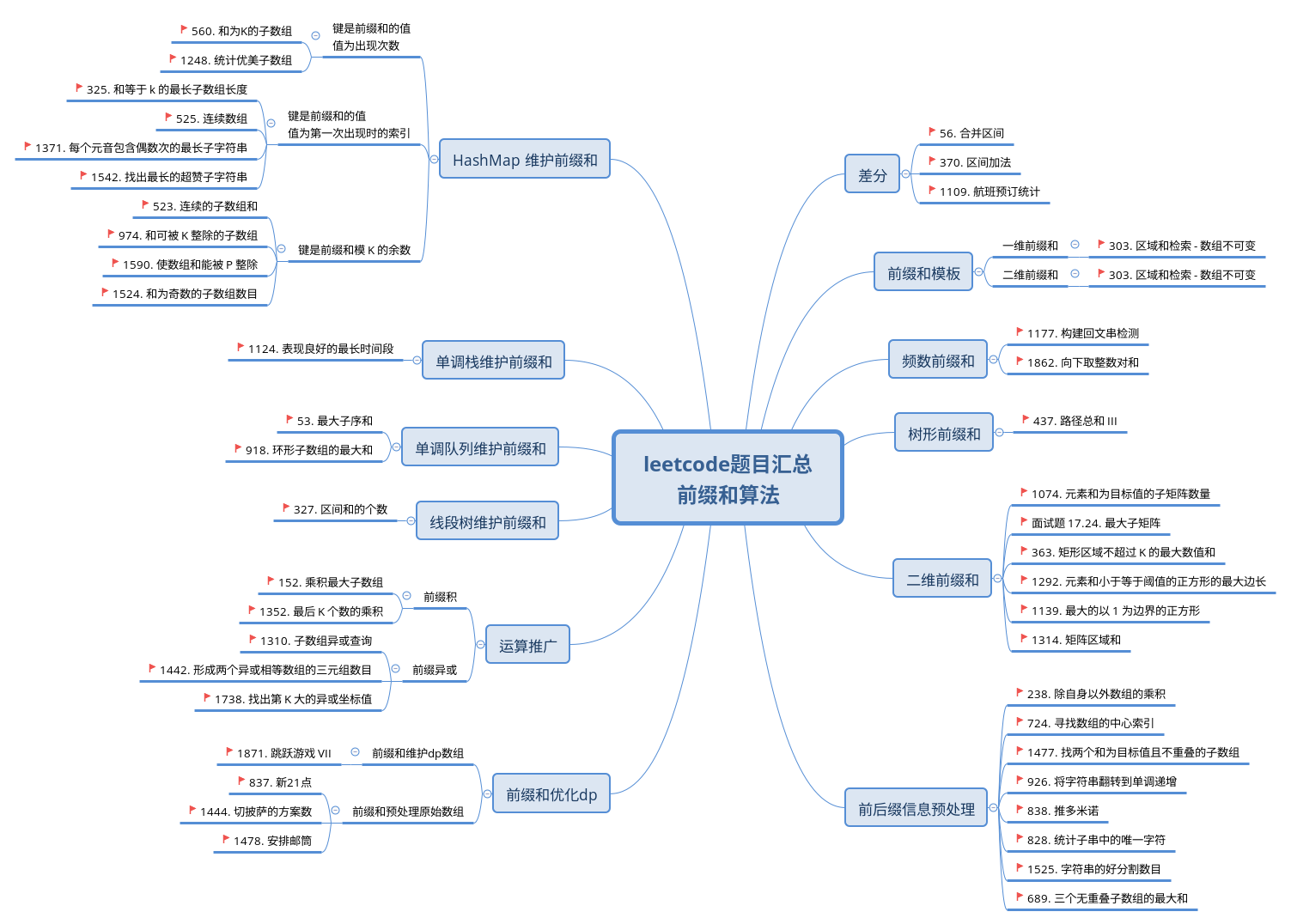
前缀和
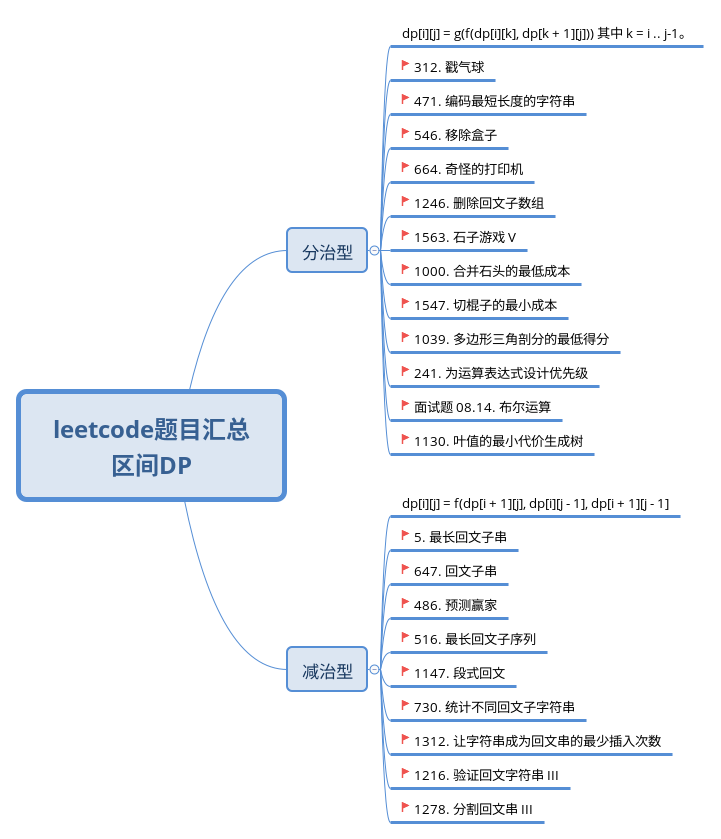
区间动态规划
对于「区间 DP」,i, j 分别是区间的左右端点,其中阶段为区间长度(j - i + 1),另外有一个是附加状态是区间左端点 i。
有的题会同时有附加维度 k。一般 k 会有长度,个数,次数,颜色等含义。
减治型
dp[i][j] 仅与常数个更小规模子问题有关,不需要枚举分割点然后两边分别求解。
一般是与 dp[i + 1][j], dp[i][j - 1], dp[i + 1][j - 1] 有关。
分治型
dp[i][j] 仅与 O(n) 个更小规模子问题有关,需要枚举分割点然后两边分别求解。
一般是枚举 [i, j] 的分割点,将区间分为 [i, k] 和 [k+1, j], 对每个 k 分别求解(下面公式的 f),再汇总(下面公式的 g)。
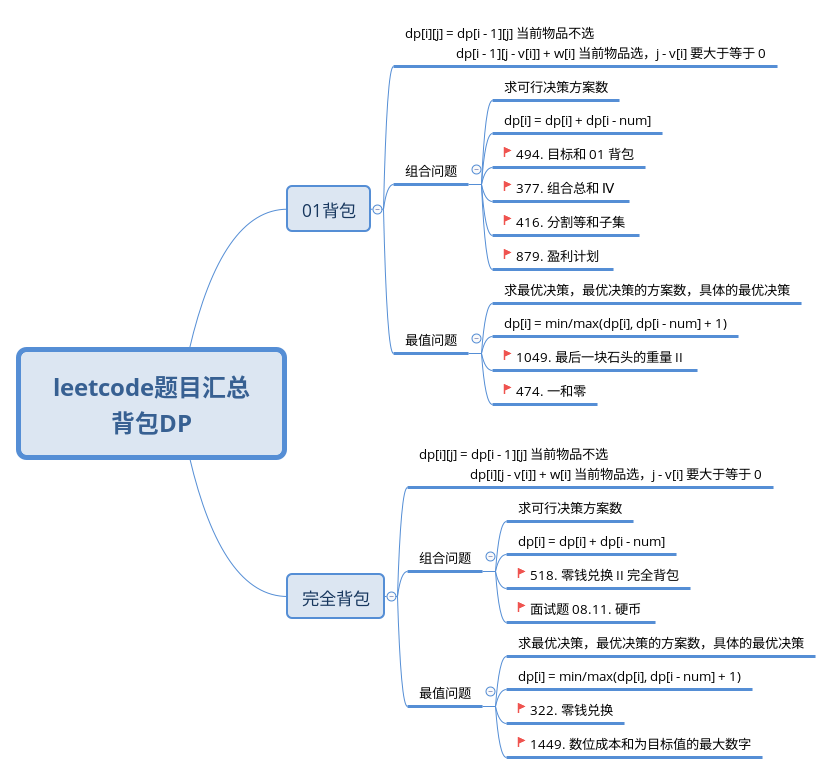
背包动态规划
对于背包问题,“已经处理的物品数”为阶段,“背包的总体积”为附加状态。
下面是 Leetcode 上与「背包 DP」相关的题目,一共十几道,分成了「01 背包」和「完全背包」、「组合问题」和「优化问题」两个维度,方便大家在刷题中感悟总结。