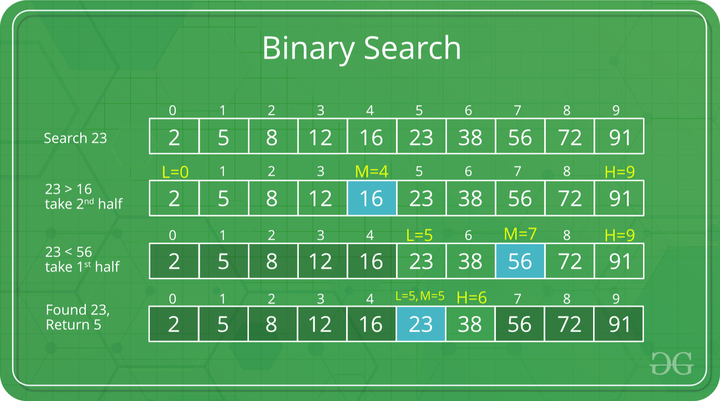
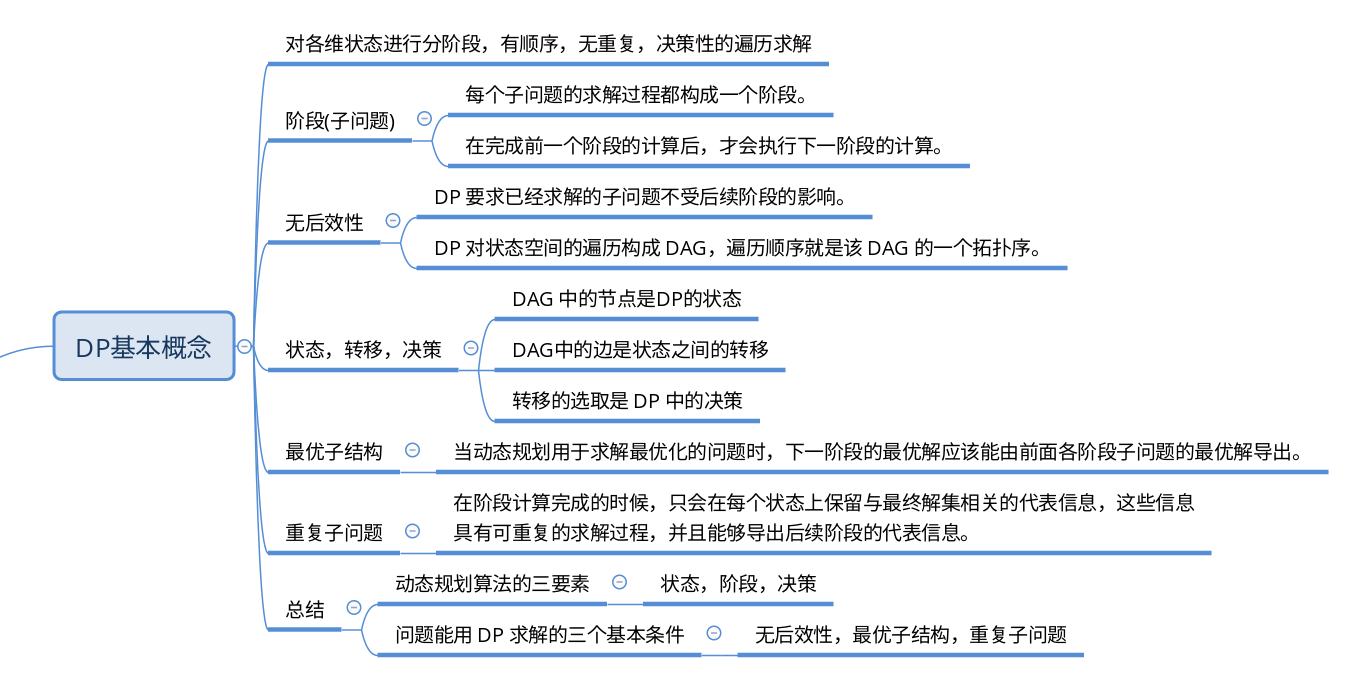
最长上升子序列(Longest Increasing Subsequence),简称 LIS,也有些情况求的是最长非降序子序列,二者区别就是序列中是否可以有相等的数。
这里详细介绍一下求LIS的三种方法,分别是O(n^2)的DP,O(nlogn)的二分+贪心法,以及O(nlogn)的树状数组优化的DP。
动态规划
设状态 dp[i] 表示 nums[0, i] 最长严格递增子序列的长度。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
int[] dp = new int[len];
Arrays.fill(dp, 1);
int res = 1;
for (int i = 0; i < len; ++i) {
for (int j = 0; j < i; ++j) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[j] + 1, dp[i]);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
|
时间复杂度:O(n^2)
贪心+二分,基于值域计算
考虑一个简单的贪心,如果我们要使上升子序列尽可能的长,则我们需要让序列上升得尽可能慢,因此我们希望每次在上升子序列最后加上的那个数尽可能的小。
直接看文字确实不太好懂,加个例子就比较容易明白,比如序列是 78912345,前三个遍历完以后 tail 是 789,这时候遍历到 1,就得把 1 放到合适的位置,于是在 tail 二分查找 1 的位置,变成了 189(如果序列在此时结束,因为 res 不变,所以依旧输出 3),再遍历到 2 成为 129,然后是 123 直到 12345。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
class Solution {
public int lengthOfLIS(int[] nums) {
int[] tails = new int[nums.length];
int res = 0;
for(int num : nums) {
int i = 0, j = res;
while(i < j) {
int m = (i + j) / 2;
if(tails[m] < num) i = m + 1;
else j = m;
}
tails[i] = num;
if(res == j) res++;
}
return res;
}
}
|
最大上升子序列之和是最长上升子序列的变种。可以用动态规划来解。
动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public int bestTeamScore(int[] scores, int[] ages) {
int len = scores.length;
Integer[] ids = new Integer[len];
for (int i = 0; i < len; ++i) {
ids[i] = i;
}
Arrays.sort(ids, (a, b) -> {
if (ages[a] == ages[b]) return scores[a] - scores[b];
return ages[a] - ages[b];
});
int res = 0;
int[] dp = new int[len];
for (int i = 0; i < len; ++i) {
int id = ids[i];
int sum = 0;
for (int j = 0; j < i; ++j) {
int idj = ids[j];
if (scores[idj] <= scores[id]) {
sum = Math.max(dp[idj], sum);
}
}
sum += scores[id];
dp[id] = sum;
res = Math.max(res, sum);
}
return res;
}
}
|
参考