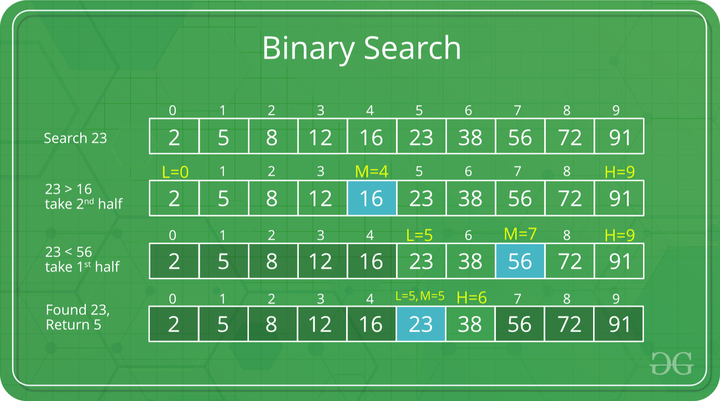
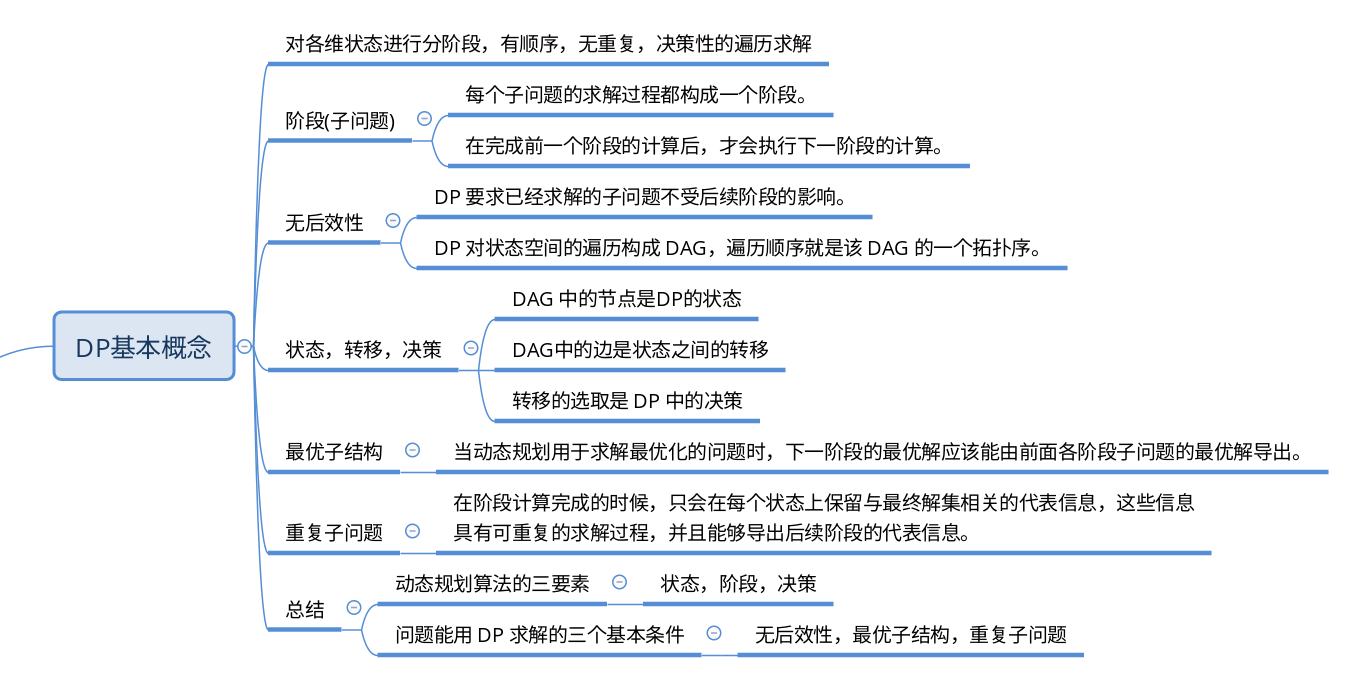
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
本文简要介绍了最长公共子序列求长度、求子序列本身及变种问题,并贴上了我自己的解答。
最长公共子序列:求长度
解题思路:见注释中的状态规划。
动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
return dp[len1][len2];
}
}
|
时间复杂度:O(len1 * len2)
空间复杂度:O(len1 * len2)
最长公共子序列:求子字符串本身
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| class Solution {
public String longestCommonSupersequence(String text1, String text2) {
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
StringBuilder sb = new StringBuilder();
int p1 = len1;
int p2 = len2;
while (p1 > 0 && p2 > 0) {
if (text1.charAt(p1 - 1) == text2.charAt(p2 - 1)) {
sb.append(text1.charAt(p1 - 1));
p1--;
p2--;
} else if (dp[p1][p2] == dp[p1 - 1][p2]) {
p1--;
} else {
p2--;
}
}
return sb.reverse().toString();
}
}
|
时间复杂度:O(len1 * len2)
空间复杂度:O(len1 * len2)
Vjudge 的例题LCS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
String text1 = sc.nextLine();
String text2 = sc.nextLine();
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
StringBuilder sb = new StringBuilder();
int p1 = len1;
int p2 = len2;
while (p1 > 0 && p2 > 0) {
if (text1.charAt(p1 - 1) == text2.charAt(p2 - 1)) {
sb.append(text1.charAt(p1 - 1));
p1--;
p2--;
} else if (dp[p1][p2] == dp[p1 - 1][p2]) {
p1--;
} else {
p2--;
}
}
System.out.println(sb.reverse().toString());
}
}
|
给出两个字符串 str1 和 str2,返回同时以 str1 和 str2 作为子序列的最短字符串。
解题思路:
- 求出最长公共子序列的长度
- 倒序求出超序字符串
- 比较两个字符是否相等:
text1.charAt(p1 - 1) == text2.charAt(p2 - 1),相等则可以使用一个字符作为公共字符。
- 确定状态转移的方向:
dp[p1][p2] == dp[p1 - 1][p2],相等则可以往 text1 方向迁移,不相等则可以往 text2 方向迁移。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
| class Solution {
public String shortestCommonSupersequence(String text1, String text2) {
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
StringBuilder sb = new StringBuilder();
int p1 = len1;
int p2 = len2;
while (p1 > 0 || p2 > 0) {
if (p1 == 0) {
sb.append(text2.charAt(--p2));
}
else if (p2 == 0) {
sb.append(text1.charAt(--p1));
}
else if (text1.charAt(p1 - 1) == text2.charAt(p2 - 1)) {
sb.append(text1.charAt(p1 - 1));
p1--;
p2--;
} else if (dp[p1][p2] == dp[p1 - 1][p2]) {
sb.append(text1.charAt(p1 - 1));
p1--;
} else {
sb.append(text2.charAt(p2 - 1));
p2--;
}
}
return sb.reverse().toString();
}
}
|
时间复杂度:O(len1 * len2)
空间复杂度:O(len1 * len2)
变种:输出所有的最长公共子序列
参考:【动态规划】输出所有的最长公共子序列
解题思路:
- 把 while 循环变成一个递归函数 helper。
- 当
dp[p1][p2 - 1] == dp[p1 - 1][p2] 时,说明可以往两个方向拓展,递归 helper 函数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| public void longestCommonSupersequenceAll(String text1, String text2) {
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i][j - 1], dp[i - 1][j]);
}
}
}
String sb = "";
int p1 = len1;
int p2 = len2;
Set<String> set = new HashSet<>();
helper(text1, text2, dp, sb, p1, p2, set);
for (String str: set)
System.out.println(str);
}
private void helper(String text1, String text2, int[][] dp, String sb, int p1, int p2, Set<String> set) {
while (p1 > 0 && p2 > 0) {
if (text1.charAt(p1 - 1) == text2.charAt(p2 - 1)) {
sb += (text1.charAt(p1 - 1));
p1--;
p2--;
} else {
if (dp[p1][p2 - 1] == dp[p1 - 1][p2]) {
helper(text1, text2, dp, sb, p1 - 1, p2, set);
helper(text1, text2, dp, sb, p1, p2 - 1, set);
return;
} else if (dp[p1][p2 - 1] > dp[p1 - 1][p2]) {
p2--;
} else {
p1--;
}
}
}
set.add((new StringBuilder(sb).reverse()).toString());
}
|
子串和子序列的区别在于,子串必须是连续的。求最长公共子串的长度和求最长公共子序列的长度的方法几乎一样,并且比最长公共子序列问题简单许多。
最长公共子串:长度或者子串本身
动态规划
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public String shortestCommonSubstring(String text1, String text2) {
int len1 = text1.length();
int len2 = text2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
int maxLen = 0;
int maxI = -1;
for (int i = 1; i <= len1; ++i) {
for (int j = 1; j <= len2; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
if (dp[i][j] > maxLen) {
maxI = i;
maxLen = dp[i][j];
}
}
}
}
if (maxLen == 0) return "";
return text1.substring(maxI - maxLen, maxI);
}
|
滑动窗口
见 LC718. 最长重复子数组 官方题解。是对动态规划的优化。
将字符串 text1 与 text2 对齐。从 text1[0] 对齐 text2[len2 - 1] 开始,直到 text1[len1 - 1] 对齐 text2[0]。
- 时间复杂度:O(len1 len2) min(len1, len2)
输出所有的最长公共字串
具体解法同上,使用一个 list 记录 maxI 即可。代码略。