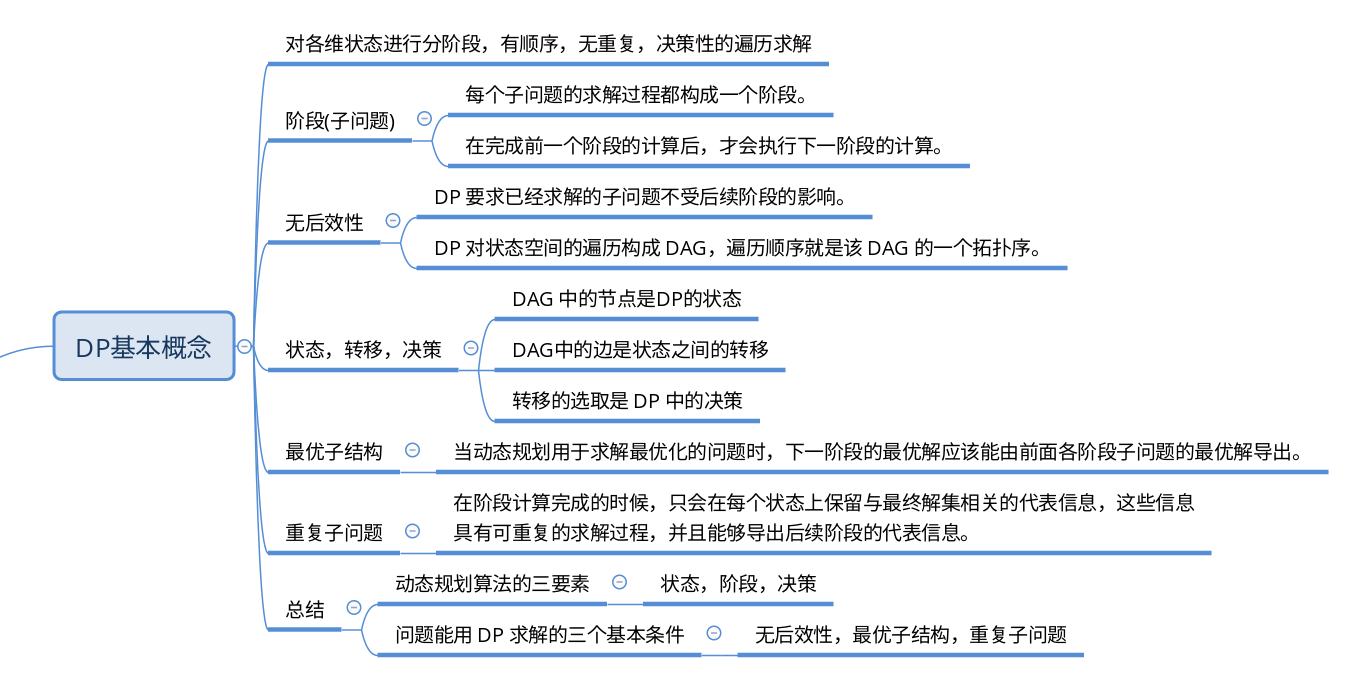
Union-Find 算法的复杂度可以这样分析：构造函数初始化数据结构需要 O(N) 的时间和空间复杂度；连通两个节点union、判断两个节点的连通性connected、计算连通分量count所需的时间复杂度均为 O(1)。

Union-Find 算法的核心逻辑如下：

  1. 用parent数组记录每个节点的父节点，相当于指向父节点的指针，所以parent数组内实际存储着一个森林（若干棵多叉树）。

  2. 用size数组记录着每棵树的重量，目的是让union后树依然拥有平衡性，保证各个 API 时间复杂度为 O(logN)，而不会退化成链表影响操作效率。

  3. 在find函数中进行路径压缩，保证任意树的高度保持在常数，使得各个 API 时间复杂度为 O(1)。使用了路径压缩之后，可以不使用size数组的平衡优化。

最终的具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class UF {
    // 连通分量个数
    private int count;
    // 存储每个节点的父节点
    private int[] parent;

    // n 为图中节点的个数
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    // 将节点 p 和节点 q 连通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);

        if (rootP == rootQ)
            return;

        parent[rootQ] = rootP;
        // 两个连通分量合并成一个连通分量
        count--;
    }

    // 判断节点 p 和节点 q 是否连通
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }

    // 路径压缩，保持树的高度平衡
    public int find(int x) {
        if (parent[x] != x) {
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 返回图中的连通分量个数
    public int count() {
        return count;
    }
}

简单: 寻找图中是否存在路径

问图中两个节点是否连通。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public boolean validPath(int n, int[][] edges, int source, int destination) {
        UnionFind uf = new UnionFind(n);
        for (int[] e: edges) {
            int s = e[0];
            int d = e[1];
            uf.union(s, d);
        }
        return uf.connected(source, destination);
    }    
}

class UnionFind {
    int[] parents;

    public UnionFind(int n) {
        this.parents = new int[n];
        for (int i = 0; i < n; ++i) {
            parents[i] = i;
        }
    }

    public void union(int p, int q) {
        int rootp = find(p);
        int rootq = find(q);
        if (rootp == rootq) return;
        parents[rootp] = rootq;
    }

    public int find(int x) {
        if (parents[x] != x) {
            parents[x] = find(parents[x]);
        }
        return parents[x];
    }

    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
}